专升本（高等数学二）模拟试卷34

一、1.选择题

0.

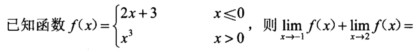
A.9
B.8
C.7
D.6

1.

A.
B.
C.
D.

2.若f’(x)＜0(α＜x≤b)且f(b)＞0，则在(α，b)内必有

A.f(x)＞0
B.f(x)＜0
C.f(x)=0
D.f(x)符号不定

3.

A.
B.
C.
D.

4.函数y=xe^x单调减少区间是

A.(-∞，0)
B.(0，1)
C.(1，e)
D.(e，+∞)

5.若x=-1和x=2都是函数f(x)=(α+x)e^b/x的极值点，则α，b分别为

A.1，2
B.2，1
C.-2，-1
D.-2，1

6.

A.
B.
C.
D.

7.

A.
B.
C.
D.

8.

A.
B.
C.
D.

9.

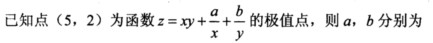
A.-50，-20
B.50，20
C.-20，-50
D.20，50

二、2.填空题

0.

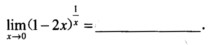
1.

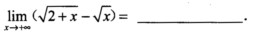
2.

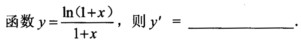
3. 函数y=lnx，则y⁽ⁿ⁾_________。

4. 若f"(1)=0且f"(1)=2，则f(1)是__________值。

5.

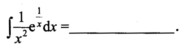
6.

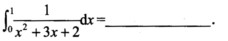
7.

8.

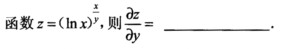
9. 求二元函数z=f(x，y)满足条件φ(x,y)=0的条件极值需要构造的拉格朗日函数为F(x，y，λ)=__________。

三、3.解答题

0.

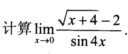
1.

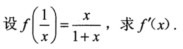
2. 已知f(x)的一个原函数是arc tanx，求∫xf"(x)dx。

3.

4. 设事件A与B相互独立，且P(A)=3/5，P(B)=q，P(A+B)=7/9，求q。

5. 当x≠0时，证明：e^x1+x。

6. 设函数y=ax³+bx+c，在点x=1处取得极小值-1，且点(0，1)是该曲线的拐点。试求常数a，b，c及该曲线的凹凸区间。

7.