通信交换技术知识点精讲之固定路由法

       >>>>>点击进入了解通信工程师网络课堂

       >>>>>点击进入了解通信工程师培训视频

       >>>>>点击进入了解通信工程师面授班

       下面是由希赛小编提供的通信交换技术知识点精讲之固定路由法，希望对学友们有所帮助。具体内容如下：

       固定路由法

       这种方法是在每个节点上保持一张路由表，表上标明去每一个‘目的节点的分组应从哪条链路进行转发。这些表是在整个系统进行配置时生成的，并且在此后的一段相当时间内保持固定不变。当网络拓扑固定不变并且通信流量也相对稳定时，采用固定路由法是适当的。

       那么如何制作这样的路由表呢？常用的方法是将网络内任何两个节点之间的最短路径事先计算好，然后根据这些最短路径制成路由表，存放在各个节点中。每一个分组都可在所到达的节点中查找到下一步应转发到哪一个节点（即下一节点或后继节点）。可见这种路由选择策略的关键就是要算出给定网络中任意两个节点之间的最短路径。

       下面介绍一种常用的求最短路径的算法，这是由Dijkstra提出的，也叫Dijkstra算法。已知条件是整个网络的拓扑和各链路的长度。

       需要指出，若将已知的各链路长度改为链路的代价或时延，这就相当于求任意两节点之间具有最小代价或最小时延的路径。因此，求最短路径的路由算法具有普遍的应用价值。

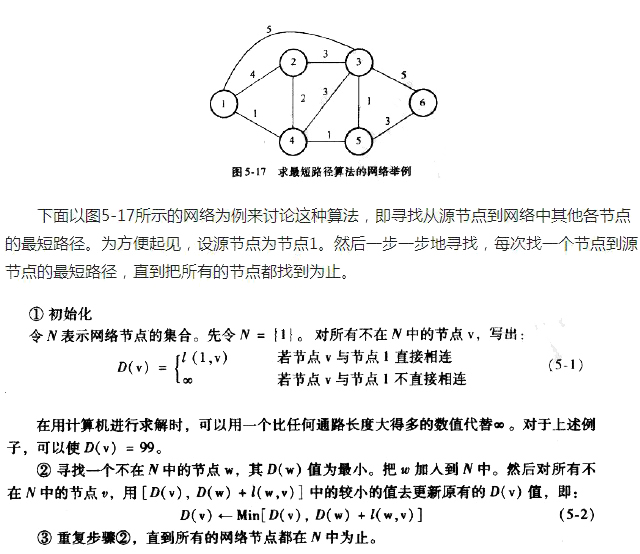
       令D(V)为源节点（节点1)到节点v的距离，它就是沿某一路径的所有链路的长度之和。再令j(i，j)为节点i至节点j之间的距离。整个算法有以下步骤。

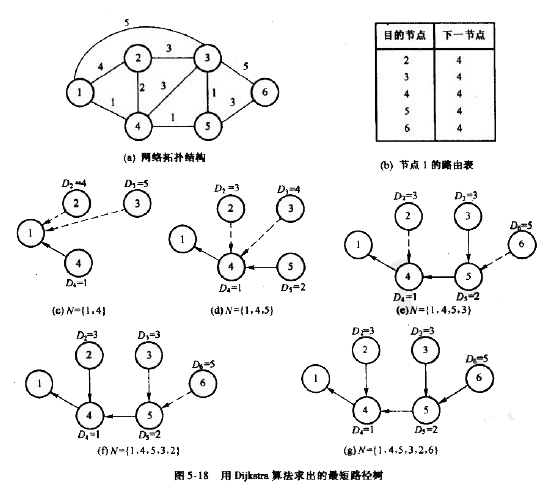
       图5-18给出了Dijkatra算法迭代求解步骤的详细图解。可以看出，上述的步骤②共执行了5次。第一次迭代找出节点1通过链路（1,4)到达节点4的距离最小，如图5-18(c)所示。第二次迭代找出下一个最近的节点是5,如图5-18(d)所示。第三次迭代找出下一个最近节点3,如图5-18(e)所示。第四次迭代找出下一个最近节点2，如图5-18(f)所示。最后一次迭代找出最后一个最近节点6,如图5-18(g)所示。至此，所有节点都包含到网络节点集合况中，计算过程即告结束。最后就得出以节点1为根的最短路径树，如图18(g)所示，于是很容易生成如图5-18(b)所示的节点1的路由表。从最短路径树可淸楚地看出从源节点（节点1)到网内任何一个节点的最短通路。此路由表指出对于发往某个目的节点的分组，从节点1发出后的下一节点应当是赛个节点。当然，像这样的路由表,在所有其他各节点中都应当有一个。但这就需要分别以这些节点为源节点，重新执行算法,然后才能找出对应的最短路径树以及相应的路由表。

       返回目录：通信交换技术知识点精讲之路由法汇总

       相关推荐：

 中级通信工程师交换技术考试真题汇总

       中级通信交换技术知识点精讲之交换网络汇总

   中级通信工程师交换技术考试培训视频推荐