MBA逻辑特殊题型：三段论的题型分配及解题方法

以下就是MBA逻辑特殊题型：三段论的题型分配及解题方法，三段论是由两个含有共同项的性质判断作为前提而得出一个新的性质判断作为结论的演绎推理，三段论由三个性质命题构成，即两个前提与一个结论。

MBA逻辑特殊题型——三段论

一、概述

1、含义

由两个含有共同项的性质判断作为前提而得出一个新的性质判断作为结论的演绎推理。

2、结构

三段论由三个性质命题构成，即两个前提与一个结论。

3、 四种标准形式

① 所有A是B，所有B是C，所有A是C。

② 有些A是B，所有B是C，有些A是C。

③ 所有A是B，所有B不是C，所有A不是C。

④ 有些A是B，所有B不是C，有些A不是C。

4、三段论传递规则

① 一特得特，不可全特。

② 一否得否，不可全否。

③ 每个词项均出现两次，中项不出现在结论中。

二、题型分类及解题方法

三段论题目的主要特征主要有两点：(1)题干和选项出现“所有”、“有些”;(2)题干至少出现三个概念，并且概念重复出现。根据题目问法的不同,将三段论的题目分为两类，即前提假设型和推出结论型。

(一)结论型

1、题型特征

题干一般会给出两个或多个前提,问可以得到什么结论。

问法为:可以推出以下哪项一定为真?

2、解题方法：文氏图法

例1：某公司所有的销售人员都是男性,所有的文秘都是女性,所有的已婚者都是文秘,公司的总经理尚未结婚。

据此,我们可以知道

A.总经理一定是男性 B.已婚者中有男性 C.女员工中可能有未婚者

D.销售人员中有的已经结婚 E.总经理一定是女性

解析: 结论型,根据题干条件画出文氏图如下：

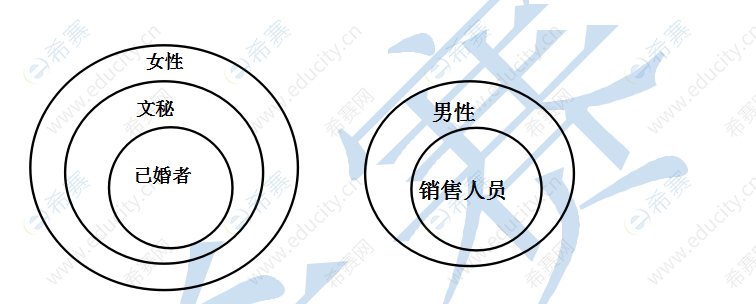
由图可知，总经理可能是男性，可能是女性，AE两项错误;已婚者都是女性，B项错误;女员工中可能有未婚者，C项正确;销售人员都未婚，D项错误。正确答案为C。

例2：所有与SARS患者接触的人都被隔离了。所有被隔离的人都与小李接触过。

如果以上命题是真的,则以下哪个命题也是真的?

A.小李是SARS患者。

B.小李不是SARS患者。

C.可能有人没有接触过SARS患者,但接触过小李。

D.所有SARS患者都与小李接触过。

E.所有与小李接触过的人都被隔离了。

解析：结论型,根据题干条件画出文氏图如下：

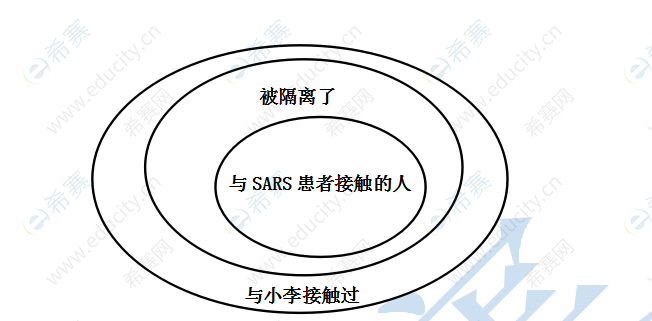
根据文氏图可知：C项为真。可能存在没有接触过SARS患者,但接触过小李的人。E项应是可能为真，不是必然为真。其他项中“小李”“SARS患者”等概念在题目信息中没有提及。正确答案为C。

(二)前提假设型

1、题型特征

题干一般会给出一个前提，以及一个结论，问想要得到结论需要补充哪项作为前提。

问法为：为使上述论证成立，以下哪项必须为真?

以下哪项陈述是上述推理必须假设的。

2、解题方法：利用三段论传递规则的特点排除。

例3：有些导演留大胡子，因此，有些留大胡子的是大嗓门。

为使上述推理成立，必须补充以下哪项作为前提?

A.有些导演是大嗓门。

B.所有大嗓门是大胡子。

C.所有导演都是大嗓门。

D.有些大嗓门不是导演。

E.有些导演不是大嗓门。

口诀：一看全特，二看肯否，三看词项。

例4：大山中学所有骑自行车上学的学生都回家吃午饭，因此，有些家在郊区的大山中学的学生不骑自行车上学。

为使上述论证成立，以下哪项关于大山中学的断定是必须假设的?

A.骑自行车上学的学生都不在郊区。

B.回家吃午饭的学生都骑自行车上学。

C.家在郊区的学生都不回家吃饭。

D.有些家在郊区的学生都不回家吃饭。

E.有些家在郊区的学生回家吃饭(E.有些不回家吃饭的学生家不在郊区)

解析：三段论补充前提型可运用三段论传递规则解决：每个词项均出现两次，中项不出现在结论中。因此“回家吃午饭”与“家在郊区的学生”需要进行联系，只有选项C、D、E满足;一否得否，不可全否，排除E项;因为E项有两次否定;一特得特，D项正确，因为D项有“有些”。正确答案为D。

(三)复合三段论—前提假设型

1、题型特征

题干一般会给出多个前提，以及一个结论，问想要得到结论需要补充哪项作为前提。

问法为：为使上述论证成立，以下哪项必须为真?

以下哪项陈述是上述推理必须假设的。

2、解题方法：先合并前提，再利用三段论传递规则的特点和排除。

合并前提：一得全特

二得肯否

三得词项

例5：所有物体实质都是可见的，而任何可见的东西都没有神秘感。因此，精神世界不是物质实体。

以下哪项最可能是上述论证所假设的?

A.精神世界是不可见的。

B.有神秘感的东西都是不可见的。

C.可见的东西都是物质实体。

D.精神世界有时也是可见的。

E.精神世界具有神秘感。

例6：没有脊索动物是导管动物，所有翼龙都是导管动物，所以，没有翼龙属于类人猿家族。

以下哪项陈述是上述推理所必须假设的?

A.所有类人猿都是导管动物。

B.所有类人猿都是脊索动物。

C.没有类人猿是脊索动物。

D.没有脊索动物是翼龙。

E.没有类人猿是导管动物。

备考公式：有些A是B = 有些B是A

                所有A不是B = 所有B不是A

                没有A是B = 所有A不是B