2018年管理类专业学位全国联考
数学
一、问题求解:第1-15小题,每小题3分,共45分。下列每题给出的A、B、C、D、E五个选项中,只有一项符合试题要求。
1. 学科竞赛设一等奖、二等奖、三等奖。比例为1:3:8,获奖率为30%,已知10人获一等奖,则参加竞赛的人数为
A.300 B.400 C.500 D.550 E.600
【参考答案】B
【答案解析】
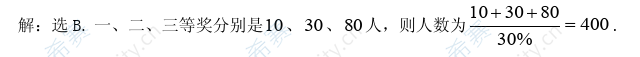
2. 为了解某公司员工的年龄结构,按男女的比例进行随机检查,结果如下:

根据表中数据估计,该公司男员工的平均年龄与全体员工的平均年龄分别是(单位:岁)
A.32,30 B.32,29.5 C.32,27 D.30,27 E.29.5,27
【参考答案】A
【答案解析】
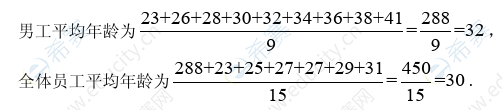
3. 某单位采取分段收费的方式收取网络流量(单位;GB)费用;每月流量20(含)以内免费。流量20-30(含)的每GB收费1元,流量30到40(含)的每GB收费3元,流量40以上的每GB收费5元。小王这个月用了45GB的流量,则他应该交费
A.45元 B.65元 C.75元 D.85元 E.135元
【参考答案】B
【答案解析】

4. 如图,圆O是三角形的内切圆,若三角形ABC的面积与周长的大小之比为1:2,则圆O的面积为
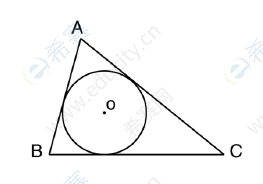
A.π B.2π C.3π D.4π E.5π
【参考答案】A
【答案解析】

5.设实数a,b满足丨a-b丨=2,丨a3-b3丨=26,则a2-b2=
A.30 B.22 C.15 D.13 E.10
【参考答案】E
【答案解析】
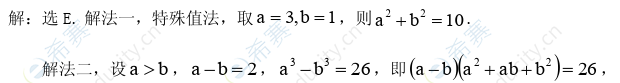
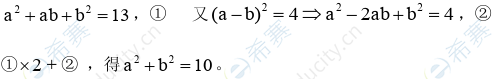
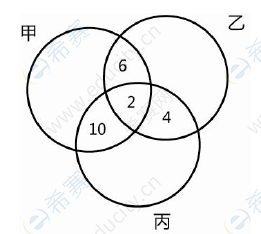
6、有96位顾客至少购买了甲、乙、丙三种商品中的一种,经调查:同时购买了甲、乙两种商品的有8位,同时购买了甲、丙两种商品的有12位,同时购买了乙、丙两种商品的有6位,同时购买了三种商品的有2位,则购买一种商品的顾客有
A.70位 B.72位 C.74位 D.76位 E.82位
【参考答案】C
【答案解析】

7.如图,四边形A1B1C1D1,A2 ,B2 ,C2 ,D2分别是A1B1C1D1 四边形的中点,A3 ,B3 ,C3,D3 分别是四边形,A2 ,B2 ,C2 ,D2 四边的中点,依次下去,得到四边形序列AnBnCnDn(n=1,2,3,...),设AnBnCnDn的面积为Sn,且S1=12,则S1+S2+S3+......=
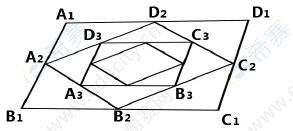
A.16 B.20 C.24 D.28 E.30
【参考答案】C
【答案解析】

8. 将6张不同的卡片2张一组分别装入甲,乙丙3个袋中,若指定的两张卡片要在同一组,则有不同的装法有
A.12种 B.18种 C.24种 D.30种 E.36种
【参考答案】B
【答案解析】

9.甲乙两人进行围棋比赛,约定先胜2盘者赢得比赛,已知每盘期甲获胜的概率是0.6,乙获胜的概率是0.4,若乙在第一盘获胜,则甲赢得比赛的概率为。
A.0.144 B.0.288 C.0.36 D.0.4 E.0.6
【参考答案】C
【答案解析】
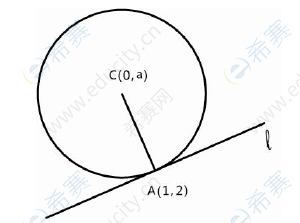
10.已知圆C:x2+(y-a)2=b,若圆C在点(1,2)处的切线与y轴的交点为(0,3),则ab=
A.-2 B.-1 C.0 D.1 E.2
【参考答案】E
【答案解析】

11. 羽毛球队有四名男运动员和三名女运动员,从中院选出两对参加混双比赛,则不同的选择方式有:
A.9种 B.18种 C.24种 D.36种 E.72种
【参考答案】D
【答案解析】

12. 从标号为1到10的10张卡片中随机抽取2张,它们的标号之和能被5整除的概率为
A.1/5 B.1/9 C.2/9 D.2/15 E.7/45
【参考答案】A
【答案解析】

13. 某单位为检查3个部门的工作,由这3个部门的主任和外聘的3名人员组成检查组。分2人组检查工作,每组有1名外聘人员,规定本部门主任不能检查本部门,则不同的安排方式
A.6种 B.8种 C.12种 D.18种 E.36种
【参考答案】C
【答案解析】

14.如图,圆柱体的底面半径为2,高为3,垂直于底面的平面截图圆柱体所截面为矩形ABCD,若弦AB所对的圆心角π∕3,则解掉部分(较小部分)的体积为

【参考答案】D
【答案解析】
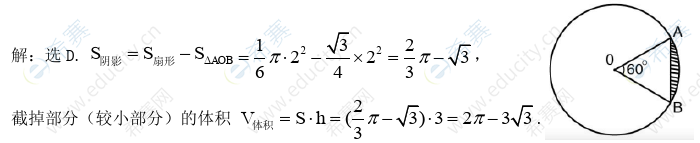
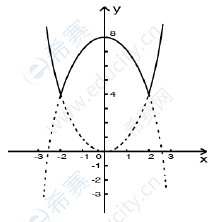
15.函数f(x)={x²,-x²+8}的最小值为
A.8 B.7 C.6 D.5 E.4
【参考答案】E
【答案解析】
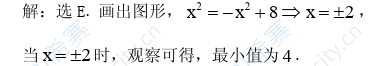
二、条件充分性判断:第16~25小题,每小题3分,共30分。要求判断每题给出的条件(1)和条件(2)能否充分支持题干所陈述的结论。A、B、C、D、E五个选项为判断结果,请选择一项符合试题要求的判断,在答题卡上将所选项的字母涂黑。
(A)条件(1)充分,但条件(2)不充分
(B)条件(2)充分,但条件(1)不充分
(C)条件(1)和(2)都不充分,但联合起来充分
(D)条件(1)充分,条件(2)也充分
(E)条件(1)和(2)都不充分,联合起来也不充分
16.设x,y为实数,则丨x+y丨≤2
(1)x2+y2≤2
(2)xy≤1
【参考答案】A
【答案解析】

17.设{an}为等差数列,则能确定a1+a2+···+a9的值
(1)已知a1的值
(2)已知a5的值
【参考答案】B
【答案解析】
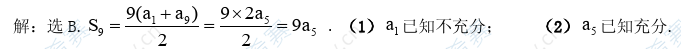

【参考答案】D
【答案解析】

19.甲、乙、丙三人的收入成等比例数列,则能确定乙的年收入的最大值
(1)已知甲、丙两人的年收入之和
(2)已知甲、丙两人的年收入之积
【参考答案】A
【答案解析】

20.如图,在矩形ABCD中,AE=FC,则三角形AED与四边形BCFE能拼成一个直角三角形
(1)EB=2FC
(2)ED=EF
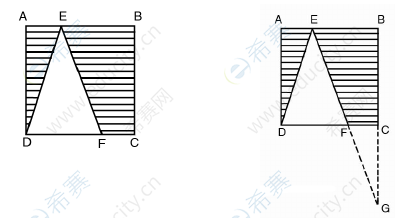
【参考答案】D
【答案解析】

21. 甲购买了若干件A玩具,乙购买了若干件B玩具送给幼儿园,甲比乙少花了100元,则能确定甲购买的玩具件数
(1) 甲比乙共购买了50件玩具
(2) A玩具的价格是B玩具的2倍
【参考答案】E
【答案解析】

22. 已知点P(m,0) A(1,3) B(2,1),点(x y)在三角形PAB上则 x-y的最小值与最大值分别为-2和
(1)m≤1 (2)m≥ -2
【参考答案】C
【答案解析】

23. 如果甲公司的年终奖总额增加25%,乙公司的年终奖总额减少10%,两者相等,则能确定两公司的员工人数之比。
(1)甲公司的人均年终奖与乙公司的相同
(2)两公司的员工人数之比与两公司的年终奖总额之比相等
【参考答案】D
【答案解析】

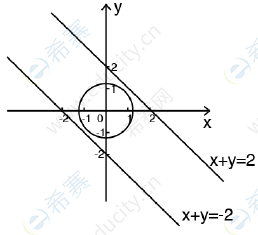
24.设a,b为实数,则圆x2+y2=2y与直线x+ay=b不想交
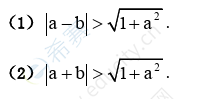
【参考答案】A
【答案解析】

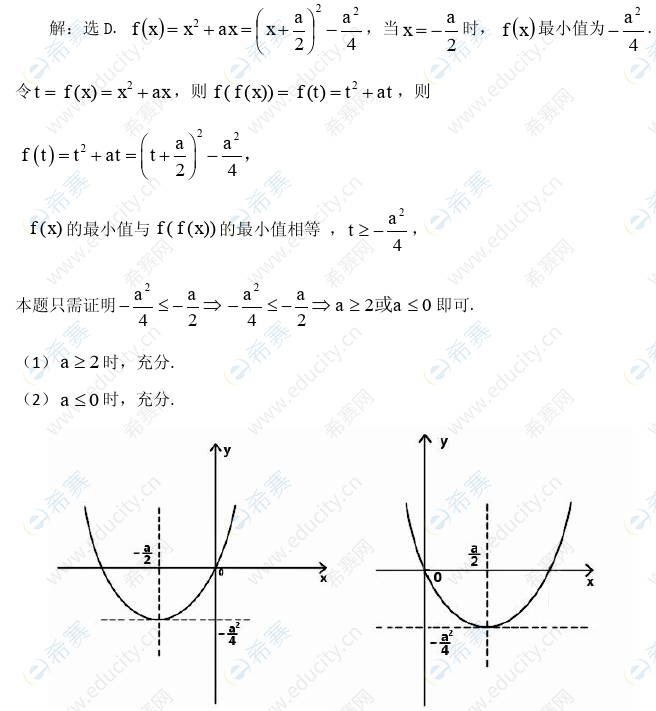
25. 设函数f(x)=x²+ax 则f(x)的最小值与f(f(x))的最小值相等
(1)a≥2
(2)a≤0
【参考答案】D
【答案解析】