湖北省普通高等学校招收中职毕业生技能高考, 是由中等职业学校(含普通中专、职业高中、技工学校和成人中专) 毕业生参加的选拔性考试,因此该考试须具有一定的信度、效度和必要的区分度。文化综合考试大纲包括语文、数学、英语三个部分。语文部分参照教育部颁布的《中等职业学校语文教学大纲》,结合我省各类中等职业学校语文教学的实际制定; 数学部分参照教育部颁布的《中等职业学校数学教学大纲》,结合我省各类中等职业学校数学教学的实际制定(数学符号使用现行国家标准); 英语部分参照教育部颁布的《中等职业学校英语教学大纲》,结合我省各类中等职业学校英语教学的实际制定。
文化综合为一份试卷, 包括语文、数学、英语三个部分,总分 210 分,其中语文、数学各 90 分,英语 30 分。考试时间 150 分钟。
第二部分 数 学
一、 考试要求
数学科目考试的宗旨是:测试考生的中学数学基础知识、 基本技能、 基本思想和方法,考查考生的中学数学基本运算能力、 逻辑思维能力, 运用所学知识分析和解决简单问题的能力.考试要求按照知识要求从低到高分为如下三个层次:
了解:初步知道知识的含义及其简单运用.
理解:懂得知识的概念和规律(定义、 定理、 法则等),以及与其他相关知识的联系.
掌握:能够运用知识的概念和规律去解决一些问题.
考试要求按照技能与能力培养要求分为三项技能与四项能力:
计算技能:根据法则、公式,或按照一定的操作步骤,正确地进行运算求解.
计算工具使用技能:正确使用科学型计算器及常用的数学工具软件.
数据处理技能:按要求对数据(数据表格)进行处理并提取有关信息.
观察能力:根据数据趋势,数量关系或图形、图示,描述其规律.
空间想象能力:依据文字、语言描述,或较简单的几何体及其组合,想象相应的空间图形;能够在基本图形中找出基本元素及其位置关系,或根据条件画出图形.
分析与解决问题能力:能对工作和生活中的简单数学相关问题,作出分析并运用适当的数学方法予以解决.
数学思维能力:依据所学的数学知识,运用类比、归纳、综合等方法,对数学及其应用问题能进行有条理的思考、判断、推理和求解;针对不同的问题(或需求),会选择合适的模型(模式) .
二、 考试内容与考核要求
第 1 章 集合与充要条件
1. 理解集合,元素,数集,空集,有限集,无限集,子集,真子集,集合相等,交集,并集,全集,补集,充分条件,必要条件,充要条件的概念.
2. 了解元素与集合的字母表示及其关系符号.
3. 掌握常用数集(自然数集、 正整数集、 负整数集、 整数集、 正有理数集、 负有理数集、 有理数集、正实数集、 负实数集、 实数集),空集,全集的字母表示.
4. 掌握集合的列举法和描述法的运用.
5. 了解平面内点集的列举法和描述法的表示.
6. 掌握非空集合所含子集,真子集,非空真子集的表示及其个数.
7. 了解子集,真子集,集合相等的表示及其关系符号.
8. 掌握交集,并集,补集的运算.
9. 掌握充分条件、 必要条件、 充要条件的判断.
第 2 章 不等式
1. 掌握比较实数大小的方法.
2. 了解不等式加法,乘法,传递的基本性质.
3. 理解区间,区间端点,开区间,闭区间,左半开区间,右半开区间,有限区间,无限区间的概念.
4. 了解开区间,闭区间,左半开区间,右半开区间,有限区间,无限区间的表示.
5. 掌握一元一次不等式,一元二次不等式,含绝对值的不等式的求解及其区间表示.
第 3 章 函数
1. 理解函数,自变量,定义域,函数值,值域,解析法,单调性,增函数,减函数,单调区间,增区间,减区间,对称轴,对称中心,奇偶性,奇函数,偶函数,非奇非偶函数,分段函数的概念.
2. 掌握函数的数形结合.
3. 掌握函数定义域的求解及其区间表示.
4. 了解函数概念中两个要素的运用.
5. 了解平面内任意点的对称点的坐标特征.
6. 掌握函数的单调性与奇偶性的判断.
7. 掌握分段函数的函数值的确定.
8. 了解函数的实际应用举例.
第 4 章 指数函数与对数函数
1. 掌握实数指数幂的运算法则.
2. 理解幂函数,指数函数,对数,对数的底,真数,常用对数,自然对数,对数函数的概念.
3. 了解幂函数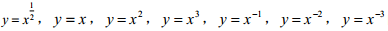 的图像与性质.
的图像与性质.
4. 了解指数函数的图像与性质.
5. 掌握对数的基本性质的运用.
6. 了解指数式与对数式的互换.
7. 了解常用对数与自然对数的简记.
8. 掌握积,商,幂的对数运算法则.
9. 了解对数函数的图像与性质.
10. 了解指数函数与对数函数的实际应用举例.
第 5 章 三角函数
1. 理解角,正角,负角,零角,任意角,象限角,界限角,终边相同的角,弧度角,角度制,弧度制,任意角的正弦函数,任意角的余弦函数,任意角的正切函数的概念.
2. 了解象限角,界限角,终边相同的角的集合表示.
3. 掌握角度与弧度的互化.
4. 掌握各象限角的正弦函数值,余弦函数值, 正切函数值的正负号的判断.
5. 掌握界限角和特殊角的正弦函数值,余弦函数值,正切函数值的确定.
6. 掌握同角正弦函数,余弦函数,正切函数的基本关系式的运用.
7. 掌握任意角的正弦函数,余弦函数,正切函数的诱导公式的运用.
8. 掌握含有正弦函数,余弦函数,正切函数的式子的化简与求值.
9. 了解正弦函数,余弦函数的图像和性质.
10. 掌握已知正弦函数值,余弦函数值,正切函数值求指定范围内特殊角的方法.
第 6 章 数列
1. 理解数列,项,首项,项数,有穷数列,无穷数列,通项或一般项, 等差数列,公差,等比数列,公比,通项公式, 前 n 项和公式的概念.
2. 了解数列通项公式的确定.
3. 了解公差,公比,通项或一般项,前 n 项和的字母表示.
4. 掌握等差数列,等比数列的通项公式和前 n 项和公式的运用.
5. 了解数列的实际应用举例.
第 7 章 平面向量
1. 理解数量,向量,向量的模,零向量,单位向量,平行(共线)向量,相等向量,自由向量,负向量,向量的加法,和向量,向量的减法,差向量,向量的数乘,向量的线性运算,向量的坐标,两个向量的夹角,向量的内积的概念.
2. 了解向量,平行(共线)向量,垂直向量,向量的内积的坐标表示.
3. 掌握向量的模的计算.
4. 掌握向量的线性运算.
5. 了解两个向量夹角的取值范围.
第 8 章 直线和圆的方程
1. 掌握任意两点间的距离公式和线段中点的坐标公式的运用.
2. 理解直线的倾斜角,斜率,横截距,纵截距,点斜式方程,斜截式方程,一般式方程,两条直线平行,两条直线重合,两条直线相交,两条直线垂直,两条直线夹角的概念.
3. 了解直线的倾斜角的取值范围.
4. 掌握经过任意两点的直线的斜率公式的运用.
5. 掌握两条直线相交的交点坐标的计算.
6. 掌握两条直线平行和两条直线垂直所满足的条件及其运用.
7. 掌握两条直线位置关系的判断.
8. 了解两条直线夹角的取值范围.
9. 掌握点到直线的距离公式的运用.
10. 掌握直线的点斜式方程,斜截式方程,一般式方程的确定.
11. 理解圆,圆心,半径,圆的标准方程,圆的一般方程的概念.
12. 了解确定圆的条件.
13. 掌握圆的标准方程和圆的一般方程的确定.
14. 掌握直线与圆的位置关系的判断.
第 9 章 立体几何
1. 了解柱、锥、球及其简单组合体的结构特征及面积、体积的计算.
第 10 章 概率与统计初步
1. 理解不可能事件,必然事件,随机事件的概念.
2. 理解频率,概率的概念.
三、 考试形式与试卷结构
1.答题方式:闭卷,笔试,不允许使用计算器.
2. 考试时间:约 60 分钟.
3. 试卷题型:包括选择题、 填空题和解答题。其中,选择题是四选一的单项选择题,填空题每题 1~2 空。全卷满分 90 分,试卷结构如下:
| 题型 | 题量 | 小题分 | 分值 |
| 选择题 | 6 | 5 | 30 |
| 填空题 | 4 | 5 | 20 |
| 解答题 | 3 | 10~15 | 40 |
| 合计 | 13 | —— | 90 |