初级会计实务知识点精讲+典型例题：即付(先付)年金的计算

即付(先付)年金的计算

即付年金，是指每期期初等额收付的年金，又称为先付年金。即付(先付)年金的计算包括：即付(先付)年金终值与即付(先付)年金现值的计算。

(1)即付年金(先付年金)终值的计算

即付年金的终值，是指把即付年金每个等额A都换算成第n期期末的数值，再来求和。

方法一：

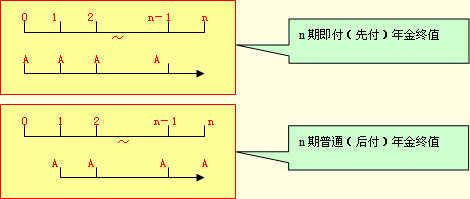
从上面可以看出，n期即付(先付)年金与n期普通(后付)年金的付款次数相同，但是由于付款时间的不同，n期即付(先付)年金终值比n期普通(后付)年金终值多计算一期利息。所以，可先求出n期普通年金的终值，然后再乘以(1+i)便可以求出n期即付年金终值。计算公式：

方法二：可根据n期即付年金终值与n+1期普通年金的终值的关系推导出另外一个公式。n期即付(先付)年金与n+1期普通(后付)年金的计息期数相同，但n期即付(先付)年金比n+1期普通(后付)年金少付一次款，因此，只要将n+1期普通(后付)年金的终值减去一期付款额A，经过整理便可以求出n期先付年金终值。即付年金的终值系数和普通年金相比，期数加1，而系数减1。计算公式：即：

【例题·计算题】某人每年年初存入银行1 000元，银行存款利率8%，求第10年末的本利和(终值)?已知：(F/A，8%，10)=14.487;(F/A，8%，11)=16.645

『正确答案』

【方法一】

F(终值)=A×年金的终值系数×(1+i)

F=A(F/A，i，n)(1+i)

F=1 000×(F/A，8%，10)×(1+8%)

=1 000×14.487×(1+8%)=15 645(元)

【方法二】

F(终值)=A× 年金的终值系数，期数加1，而系数减1

F=A[(F/A，i，n+1)-1]

F=A[(F/A，i，n+1)-1]

=1 000×[(F/A，8%，11)-1]

=1 000×(16.645-1)

=15 645(元)

【例题·计算题】为给儿子上大学准备资金，王先生连续6年于每年年初存入银行3 000元。若银行存款利率为5%，则王先生在第6年末能一次取出本利和多少钱?

『正确答案』

【方法一】

F(终值)=A×年金的终值系数×(1+i)

F=A(F/A，i，n)(1+i)

F=3 000×(F/A，5%，6)×(1+5%)=21 426(元)

【方法二】

F(终值)=A× 年金终值系数，期数加1，而系数减1

F=A[(F/A，i，n+1)-1]

F=A[(F/A，i，n+1)-1]

=3 000×[(F/A，5%，7)-1]

=3 000×(8.1420-1)

=21 426(元)

【例题·计算题】孙女士看到在邻近的城市中，一种品牌的火锅餐馆生意很火爆。她也想在自己所在的县城开一个火锅餐馆，于是找到业内人士进行咨询。花了很多时间，她终于联系到了火锅餐馆的中国总部，总部工作人员告诉她，如果她要加入火锅餐馆的经营队伍，必须一次性支付50万元，并按该火锅品牌的经营模式和经营范围营业。孙女士提出现在没有这么多现金，可否分次支付，得到的答复是如果分次支付，必须从开业当年起，每年年初支付20万元，付3年。3年中如果有一年没有按期付款，则总部将停止专营权的授予。假设孙女士现在身无分文，需要到银行贷款开业，而按照孙女士所在县城有关扶持下岗职工创业投资的计划，她可以获得年利率为5%的贷款扶持。请问孙女士现在应该一次支付还是分次支付?

『正确答案』对孙女士来说，如果一次支付，则相当于付现值50万元;而若分次支付，则相当于一个3年的即付年金，孙女士可以把这个即付年金折算为3年后的终值，再与50万元的3年终值进行比较，以发现哪个方案更有利。

(1)如果分次支付，则其3年终值为：

F(终值)=A×年金的终值系数×(1+i)

F=20×(F/A，5%，3)×(1+5%)

=20×3.1525×1.05

=66.2025(万元)

或者：F(终值)=A× 年金的终值系数，期数加1，而系数减1

F=20×[(F/A，5%，4)-1]

=20×(4.3101-1)

=66.202(万元)

(2)如果一次支付，则其3年的终值为：

F(终值)=P(现值)×复利终值系数

50×(F/P，5%，3)=50×1.1576=57.88(万元)

相比之下，一次支付效果更好。

更多初级会计实务知识点请阅读：初级会计实务知识点精讲+典型例题汇总